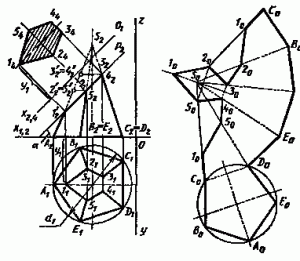
Развертка усеченной пирамиды
Развертка усеченной пирамиды. Следует построить полную развертку боковой поверхности пирамиды SABCDE. Натуральные величины граней такой пирамиды определять нет необходимости. Ребра одинаковые, и натуральная величина одного из ребер SA имеется на фронтальной плоскости проекции.
Развертка боковой поверхности всей пирамиды строится так же. Для нанесения на развертку точек 2, 3, 4, 5 необходимо перенести их на натуральную величину ребра SA. Это точки 2'2, 32, 4'г, 5'2, а точка 1 находится на ребре SA. Затем следует измерить натуральные величины S2I2, 5г22, S232, S^, S25'2 и отложить их на соответствующих ребрах на развертке. После построения развертки боковой поверхности усеченной части пирамиды следует пристроить к ней пя¬тиугольник A^CJD^E^ — основание пирамиды и на¬туральную величину сечения 12 345, которая может быть определена одним из способов преобразования чертежа (в большинстве случаев способом замены плоскостей про¬екций). Для этого на фронтальной плоскости проекции параллельно плоскости Р2 проводим новую ось проекций хгА и переносим все точки 1, 2, 3, 4, 5 в новую систему плоскостей; при этом расстояния у переносим из старой системы координат.
Развертка конической поверхности. Задача на построение развертки конической поверхности решается так же, как в случае построения развертки боковой поверхности пирамиды способом треугольника. Если задана поверхность прямого кругового конуса, то развертка его боковой поверхности представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности / = | SA |, а центральный угол <р = 2пг[1, где г — радиус окружности основания конуса.